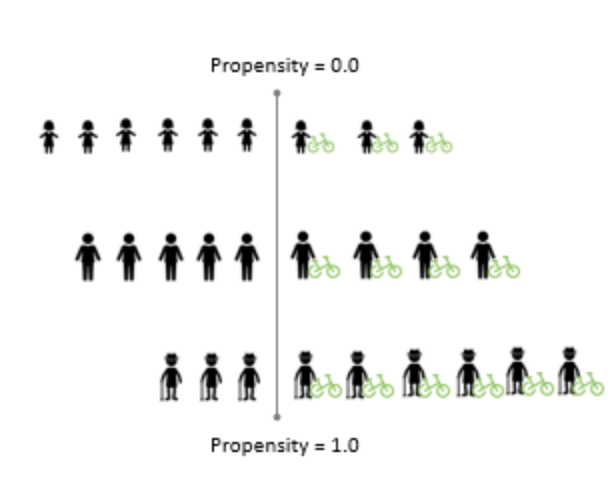
Propensity Score Weighting

• 작성자: 김가연

---

성향점수 가중(Propensity Score Weighting) 은 처치집단의 성향점수와 통제집단의 성향점수가 같아지도록 가중치를 부여하는 방법입니다.

아래 그림은 앞서 다뤘던 운동 여부에 따른 콜레스테롤 수치 비교 사례로, 일반적으로 처치집단에는 성향점수가 높은 개체가, 비교집단에는 성향점수가 낮은 개체가 과대표집 되었을 가능성이 큽니다.

성향점수가 높은 개체가 처치집단에, 낮은 개체가 비교집단에 과대표집 (출처: kdd-tutorial 2018)

따라서 과대표집에 대한 균형을 맞추고자 각 집단에 다른 가중치를 부여해 처치효과를 추정합니다.

DoWhy 라이브러리의 propensity_score_weighting_estimator 모듈에서는 가중치를 부여하는 방법으로 inverse propensity score (’ips_weight’), stabilized IPS score (’ips_stabilized_weight’), normalized IPS score (’ips_normalized_weight’) 총 3가지를 제공합니다.

# dowhy.causal_estimators.propensity_score_weighting_estimator _estimate_effect 함수 코드 일부

# ips_weight
self._data['ips_weight'] = (1/num_units) * (
    self._data[self._treatment_name[0]] / self._data['ps'] +
    (1 - self._data[self._treatment_name[0]]) / (1 - self._data['ps'])
)
self._data['tips_weight'] = (1/num_treatment_units) * (
    self._data[self._treatment_name[0]] +
    (1 - self._data[self._treatment_name[0]]) * self._data['ps']/ (1 - self._data['ps'])
)
self._data['cips_weight'] = (1/num_control_units) * (
    self._data[self._treatment_name[0]] * (1 - self._data['ps'])/ self._data['ps'] +
    (1 - self._data[self._treatment_name[0]])
)

# ips_normalized_weight
self._data['ips_normalized_weight'] = (
    self._data[self._treatment_name[0]] / self._data['ps'] / ipst_sum +
    (1 - self._data[self._treatment_name[0]]) / (1 - self._data['ps']) / ipsc_sum
)
ipst_for_att_sum = sum(self._data[self._treatment_name[0]])
ipsc_for_att_sum = sum((1-self._data[self._treatment_name[0]])/(1 - self._data['ps'])*self._data['ps'] )
self._data['tips_normalized_weight'] = (
    self._data[self._treatment_name[0]]/ ipst_for_att_sum  +
    (1 - self._data[self._treatment_name[0]]) * self._data['ps'] / (1 - self._data['ps']) / ipsc_for_att_sum
)
ipst_for_atc_sum = sum(self._data[self._treatment_name[0]] / self._data['ps'] * (1-self._data['ps']))
ipsc_for_atc_sum = sum((1 - self._data[self._treatment_name[0]]))
self._data['cips_normalized_weight'] = (
    self._data[self._treatment_name[0]] * (1 - self._data['ps']) / self._data['ps'] / ipst_for_atc_sum +
    (1 - self._data[self._treatment_name[0]])/ipsc_for_atc_sum
)

# ips_stabilized_weight
p_treatment = sum(self._data[self._treatment_name[0]])/num_units
self._data['ips_stabilized_weight'] = (1/num_units) * (
    self._data[self._treatment_name[0]] / self._data['ps'] * p_treatment +
    (1 - self._data[self._treatment_name[0]]) / (1 - self._data['ps']) * (1- p_treatment)
)
self._data['tips_stabilized_weight'] = (1/num_treatment_units) * (
    self._data[self._treatment_name[0]] * p_treatment  +
    (1 - self._data[self._treatment_name[0]]) * self._data['ps'] / (1 - self._data['ps']) * (1- p_treatment)
)
self._data['cips_stabilized_weight'] = (1/num_control_units) * (
    self._data[self._treatment_name[0]] * (1 - self._data['ps']) / self._data['ps'] * p_treatment +
    (1 - self._data[self._treatment_name[0]])* (1-p_treatment)
)

# ATE, ATT, ATC 에 따라 다른 가중치 부여 방법
if self._target_units == "ate":
    weighting_scheme_name = self.weighting_scheme
elif self._target_units == "att":
    weighting_scheme_name = "t" + self.weighting_scheme
elif self._target_units == "atc":
    weighting_scheme_name = "c" + self.weighting_scheme
else:
    raise ValueError("Target units string value not supported")

# 처치효과 계산
self._data['d_y'] = ( # 처치집단 가중치 * outcome
    self._data[weighting_scheme_name] *
    self._data[self._treatment_name[0]] *
    self._data[self._outcome_name]
)
self._data['dbar_y'] = ( # 비교집단 가중치 * outcome
    self._data[weighting_scheme_name] *
    (1 - self._data[self._treatment_name[0]]) *
    self._data[self._outcome_name]
)
est = self._data['d_y'].sum() - self._data['dbar_y'].sum()

성향점수 가중 방법은 성향점수의 역수를 가중치로 적용하여 처치집단과 비교집단에 배치될 확률을 동일하게 만듭니다. 예를 들어 ATE 를 추정하는 경우, 아래 식과 같이 성향점수(PS(X))가 높을수록 처치집단(T)에 속한 개체는 작은 가중치(W)를, 비교집단(1-T)에 속한 개체는 큰 가중치(W)를 갖게 합니다.

$$W = T*(1/PS(X)) + (1-T)*(1/(1-PS(X)))$$

이렇듯 성향점수의 역수를 활용하여 통계적 의미에서 실험적 설계 상황을 설정하게 함으로써 데이터가 관심 모집단 특성을 갖추도록 하는데 용이합니다. 다만 극단적 가중치의 영향을 받을 수 있어, 10보다 큰 가중치는 제외하고 분석하거나 성향점수의 상·하위 각 2.5%에 해당하는 개체를 제외하고 분석하는 방법이 있습니다.